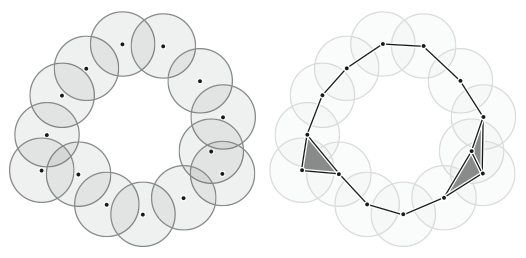
Often, high dimensional data lie close to a low-dimensional submanifold and it is of interest to understand the geometry of these submanifolds. The homology groups of a manifold are important topological invariants that provide an algebraic summary of the manifold. These groups contain rich topological information, for instance, about the connected components, holes, tunnels and sometimes the dimension of the manifold. In this paper, we consider the statistical problem of estimating the homology of a manifold from noisy samples under several different noise models. We derive upper and lower bounds on the minimax risk for this problem. Our upper bounds are based on estimators which are constructed from a union of balls of appropriate radius around carefully selected points. In each case we establish complementary lower bounds using Le Cam's lemma.

@article{balakrishnan12minimax,
  Title     = {Minimax rates for homology inference},
  Author    = {Sivaraman Balakrishnan and
               Alessandro Rinaldo and
               Don Sheehy and
               Aarti Singh and
               Larry A. Wasserman},
  Journal   = {Journal of Machine Learning Research - Proceedings Track},
  Volume    = {22},
  Pages     = {64--72},
  Year      = {2012}}