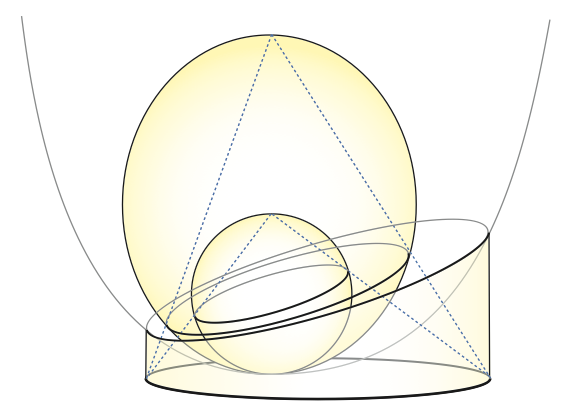
A geometric separator for a set $U$ of $n$ geometric objects (usually balls) is a small (sublinear in $n$) subset whose removal disconnects the intersection graph of $U$ into roughly equal sized parts. These separators provide a natural way to do divide and conquer in geometric settings. A particularly nice geometric separator algorithm originally introduced by Miller and Thurston has three steps: compute a centerpoint in a space of one dimension higher than the input, compute a conformal transformation that ``centers'' the centerpoint, and finally, use the computed transformation to sample a sphere in the original space. The output separator is the subset of $S$ intersecting this sphere. It is both simple and elegant. We show that a change of perspective (literally) can make this algorithm even simpler by eliminating the entire middle step. By computing the centerpoint of the points lifted onto a paraboloid rather than using the stereographic map as in the original method, one can sample the desired sphere directly, without computing the conformal transformation.

@inproceedings{sheehy13geometric,
  Title = {Geometric Separators and the Parabolic Lift},
  Author = {Donald R. Sheehy},
  Booktitle = {Canadian Conference in Computational Geometry},
  Pages = {253--258}
  Year = {2013}}