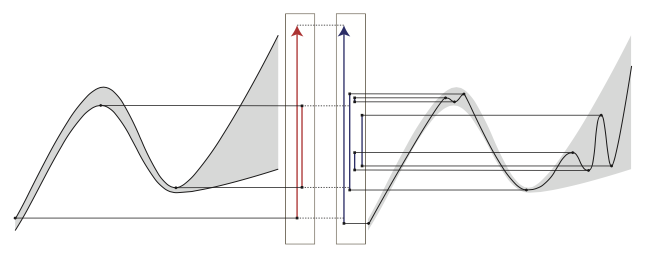
From the work of Bauer and Lesnick, it is known that there is no functor from the category of pointwise finite-dimensional persistence modules to the category of barcodes and overlap matchings. In this work, we introduce sub-barcodes and show that there is a functor from the category of factorizations of persistence module homomorphisms to a poset of barcodes ordered by the sub-barcode relation. Sub-barcodes and factorizations provide a looser alternative to bottleneck matchings and interleavings that can give strong guarantees in a number of settings that arise naturally in topological data analysis. The main use of sub-barcodes is to make strong claims about an unknown barcode in the absence of an interleaving. For example, given only upper and lower bounds $g\ge f\ge\ell$ of an unknown real-valued function $f$, a sub-barcode associated with $f$ can be constructed from $\ell$ and $g$ alone. We propose a theory of sub-barcodes and observe that the subobjects in the category of functors from intervals to matchings naturally correspond to sub-barcodes.

@misc{https://doi.org/10.48550/arxiv.2206.10504,
  author = {Oliver A. Chubet and Kirk P. Gardner and Donald R. Sheehy},
  title = {A Theory of Sub-Barcodes},
  doi = {10.48550/ARXIV.2206.10504},
  url = {https://arxiv.org/abs/2206.10504},
  publisher = {arXiv},
  year = {2022},
}