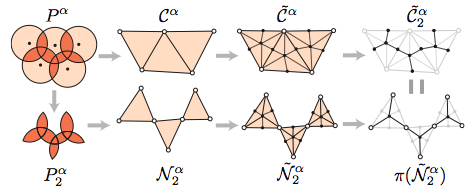
We show that filtering the barycentric decomposition of a \v Cech complex by the cardinality of the vertices captures precisely the topology of $k$-covered regions among a collection of balls for all values of $k$. Moreover, we relate this result to the Vietoris-Rips complex to get an approximation in terms of the persistent homology.

@inproceedings{sheehy12multicover,
  Title = {A Multicover Nerve for Geometric Inference},
  Author = {Donald R. Sheehy},
  Booktitle = {CCCG: Canadian Conference in Computational Geometry},
  Pages = {309--314},
  Year = {2012}}